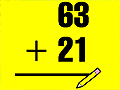среда, 18 мая 2011 г.
Задача на логику "Поменяй местами!"
Новая задачка про лягушек. На первый взгляд, не сложно поменять их местами, но не тут то было - попробуйте! Итак, развиваем логику! Приятного времяпровождения!
РЕШЕНИЕ
Я умею складывать!
Замечательная флэш-игра для Ваших ребятишек на отработку навыков сравнения и сложения чисел, а также закрепление понятий слагаемое и сумма.
Парадокс Монти-Холла
Этот парадокс настолько популярен, что его можно встретить в художественной литературе (С. Лукьяненко в книге "Недотепа"), а также при просмотре фильмов "Числа" и "Двадцать одно".
Сюжет из видеофильма "Двадцать одно":
Из сюжета видно: правильный ответ - это изменить свой выбор. И это действительно так: конечно это не значит, что Вы выиграли машину, но вероятность выигрыша увеличилась от 33,3% до 66,6%. Могу точно сказать, что парадокс Монти-Холла работает!
РЕШЕНИЕ
В статье"Парадокс Монти-Холла" менять или не менять свое решение при новых условиях игры, мы выяснили, что правильный ответ - это изменить свой выбор. Почему изменить? Объясняю - предположим у Вас есть выбор: идти направо, где Вы наткнетесь на три двери, за двумя из которых автомобили, а за третьей коза или налево, где тоже три двери, но за двумя из них козы и за одной автомобиль. Куда пойдете Вы? Думаю, что направо. Ведь глупо идти туда, где меньше шансов! Изменение условий в процессе данной игры тоже приводит человека к вышеописанной ситуации, когда у Вас есть выбор: направо с двумя машинами и налево с одной. Правда попав в игру или похожую жизненную ситуацию обычно человек этого не видит, какая разница эта или другая дверь - ведь все-равно за одной из них машина, а за другой коза. Для большинства людей это кажется настолько правдивым, что когда им говорят: надо изменить свой выбор и это единственно правильное решение, то этот вывод оказывается противоречит их интуитивному восприятию данной ситуации, кстати именно поэтому описанная задача и называется парадоксом. Я уже писала в одной из первых статей, что парадокс - это всегда полуправда или полувымысел. А раз решение нам известно, и оно точно верное, то к парадоксу получается и не относится и парадокс Монти-Холла заключается в том, что человек, оказавшись в данной ситуации противоречит своим решением правильному ответу.
Итак, объясню парадокс самым простым языком:
Перед Вами три двери - за двумя находятся козы, а за одной автомобиль. Вы делаете выбор, а значит Вы счастливый обладатель козы или не менее счастливый владелец автомобиля. Но что же за дверью? Вам уже не терпится это узнать, но вдруг ведущий открывает одну из оставшихся дверей, за которой точно нет автомобиля и перед Вами ситуация: 50 на 50. Вы можете оставить свой выбор или изменить его. И вот тут самое интересное:
1.Предположим, вы не меняете свой выбор. В таком случае возможны три варианта:
- если Вы изначально выбрали автомобиль (пусть это будет первая дверь), то я Вас поздравляю с приобретением машины;
- если Вы изначально выбрали козу №1 (пусть это будет вторая дверь), то я Вас поздравляю с приобретением козы;
- если, Вы изначально выбрали козу №2 (пусть это будет третья дверь), то и в этом случае я поздравлю Вас с козой;
Вывод: Если Вы остались при своем мнение, то Вы пошли налево, где как помнится за двумя дверьми козы и за одной автомобиль, а значит вероятность выигрыша автомобиля 1/3.
2. Вы меняете свое решение. В таком случае другие три варианта:
- если Вы изначально выбрали автомобиль (пусть это опять будет первая дверь), то к сожалению Вам придется, по нашему условию, изменить свой выбор в пользу козы, которая за второй или третьей дверью, а впрочем это не важно, Ваш приз все равно коза;
- если Вы изначально выбрали козу №1 (пусть это будет вторая дверь), то, меняя свое мнение, естественно в пользу автомобиля, т.к. вторую козу ведущий из игры исключает Вы становитесь обладателем автомобиля;
- если Вы изначально выбрали козу №2 (пусть это будет третья дверь), то, меняя свое мнение, естественно опять в пользу автомобиля, т.к. первую козу ведущий из игры в этом случае исключает Вы становитесь обладателем автомобиля;
Вывод: Если Вы изменили свое мнение, то Вы пошли направо, где как помнится за двумя дверьми автомобили и за одной коза, а значит вероятность выигрыша автомобиля 2/3.
Если и это объяснение Вас не убедило, то у Вас два варианта: либо просто принять это как факт, либо довольствоваться 33,3%. Хотя могуц предложить еще один вариант: проверьте это опытным путем, поиграв в эту игру следующим образом сначала 10 раз подряд не меняйте свое решение, а потом 10 раз подряд - меняйте. Думаю, результат все сам скажет за себя!
вторник, 17 мая 2011 г.
Умножение графическим способом
Я уже показывала как на пальцах можно умножать числа на 6,7,8 и 9. Пальцев для многозначных чисел не хватит, поэтому берем листок бумаги и карандаш.
Итак, умножение многозначных чисел.
На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера.
Умножение на палочках
Сначала 32: 3 красные линии и чуть ниже - 2 синие. Затем 21: перпендикулярно уже нарисованным, рисуем сначала 2 зеленые, затем - 1 малиновую. ВАЖНО: линии первого числа рисуются в направлении из верхнего левого угла в нижний правый, второго числа - из нижнего левого, в верхний правый. Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области обозначены в виде окружностей). Итак, в первой области ( область сотен) - 6 точек, во второй (область десятков) - 7 точек, в третьей (область единиц) - 2 точки. Следовательно ответ: 672.
Разберем другой пример: 123х412=50676
Умножение на палочках
В школе достаточно часто просят решить какую либо задачу несколькими способами: аналитическим, графическим..., но не умножение многозначных чисел, такой способ умножения не имеет право на жизнь в школе, там умножают обычно в столбик, но это не значит, что он не заслуживает внимания.
Математическая атака
Флэш-игра для детей начальной школы для отработки навыков сложения, вычитания, умножения и деления с числами до ста. Умение быстро и главное правильно оперировать основными действиями в математике очень важно. В школах-лицеях в начальных классах проводят математические диктанты, где на скорость надо решать предложенные примеры. Скорость и правильность решения ваших детей пригодиться в старших классах, ведь там уже надо изучать более сложные вещи. чем решение подобных примеров.
ИГРАТЬ
ИГРАТЬ
Поэтическая минутка. Математика.
Высота, медиана и биссектриса треугольника
Три девицы, три сестрицы
В треугольнике живут.
Речь такую там ведут:
— Всех главнее высота!
Говорю вам неспроста.
Видят все, как сторонам
Нужен перпендикуляр.
Тогда они, сменив названья,
Зовутся гордо — основанья!
— Нет, — сказала медиана, —
Спорить я не перестану.
И на это есть причина:
Я треугольника вершину
Соединяю с серединой
Стороны. К тому же я
Делю всю площадь пополам!
В спор вступила биссектриса:
— Спорить не имеет смысла!
Если трое соберемся,
В точке мы пересечемся.
Эта точка непростая.
Серединка золотая;
Если циркулем владеешь,
Окружность ты списать сумеешь!
Значит, всех я вас главнее!
В спор вмешался треугольник:
— Что вы, знает каждый школьник,
Что для меня вы все равны.
Будьте же всегда дружны!
Но вас предупреждаю я:
У каждой миссия своя!
Знает каждый школьник,
Как меня построить.
К чему не проведут меня,
Всем перпендикулярна я.
Отгадай, вопрос простой,
Как зовусь я? (Высотой).
Вначале вы найти должны
Середину стороны.
Ее соединишь с вершиной,
И меня уж получил ты.
Просто все и без обмана.
Как зовусь я? (Медиана).
Определение косинуса, синуса, тангенса и котангенса острого угла в прямоугольном треугольнике
Шарада
Что кружится, что ложится
И на землю, и на крыши,
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко.
А второе просто «на».
Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось,
И прочти наоборот.
Не запутайся, читая
Слово задом наперед!
(Снег-на-ток... котангенс).
С тригонометрией сейчас
Знакомы даже звери.
Правила все говорят
Четко и уверенно.
И попросим мы зверят
Рассказать их для ребят.
Как мы косинус считаем,
Ты спроси медузу.
— Делим прилежащий катет
На гипотенузу.
Синус вычислить сумеет
Зверь любой из лесной чащи:
На гипотенузу делит
Катет противолежащий.
Чтобы тангенс получить,
Нужно катеты делить.
Вы в числителе берете
Тот, что для угла напротив.
Тот, который прилежит,
В знаменателе пиши.
Если дробь перевернуть,
Это тоже верный путь!
Ты с конца прочти, дружок,
Как ложится «снег на ток».
— Как назвали отношенье катета к гипотенузе?
У кого ни спросим мы,
Отвечают: «Косинус».
Все мы думали-гадали:
Какой же они катет брали?
Площади многоугольников
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.
ПИФАГОРОВА ТЕОРЕМА
Не знаю, чем кончу поэму,
И как мне печаль избыть;
Древнейшую теорему
Никак я не в силах забыть.
Стоит треугольник, как ментор,
И угол прямой в нем есть.
И всем его элементам
Повсюду покой и честь.
Прелестная гипотенуза
Вознеслась так смело ввысь!
И с нею в вечном союзе
Два катета тоже взнеслись.
Она царит на квадратах
И песню поет она.
Та песня влечет куда-то
Геометров древних волна.
И все на торжищах света,
Как в огненном кольце,
И все повторяют это:
Ах, а, в, с!
И даже в холодной медузе
Огонь эта песня зажгла,
И все это гипотенузы
И катетов двух дела!
О ТЕОРЕМЕ ПИФАГОРА
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в далекий век.
Обильно было жертвоприношенье
Богам от Пифагора: сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет —
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
ГИМН ГИПОТЕНУЗЕ
Как символ вечного союза,
Как вечный символ знак простой,
Связала гипотенуза
Навеки катеты собой.
Путей окольных избегая
И древней истине верна,
Ты по характеру — прямая
И по обычаю — точна.
Скрывала тайну ты, но скоро
Явился некий мудрый грек
И теоремой Пифагора
Тебя прославил он навек.
Хранит тебя, безмолвно, чинно
Углов сторожевой наряд,
И копья — острые вершины
На обе стороны грозят.
И если двоечник, конфузясь,
Немеет пред твоим лицом.
Пронзит его, гипотенуза,
Своим отточенным копьем.
БАЛЛАДА О МАТЕМАТИКЕ
Как воздух, математика нужна,
Самой отваги офицеру мало.
Расчеты! Залп! И цель поражена
Могучими ударами металла.
И воину припомнилось на миг,
Как школьником мечтал в часы ученья:
О подвиге, о шквалах огневых,
О яростном порыве наступленья. .
Но строг учитель был,
И каждый раз он обрывал мальчишку грубовато:
— Мечтать довольно, повтори рассказ
О свойствах круга и углах квадрата.
И воином любовь сохранена
К учителю далекому, седому.
Как воздух, математика нужна
Сегодня офицеру молодому.
О НУЛЕ
Когда-то многие считали,
Что нуль не значит ничего.
И как ни странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел
Он все же место получил.
И все действительные числа
На два разряда разделил.
Коль нуль к числу ты прибавляешь,
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав, как множитель, средь чисел
Он сводит мигом все на нет.
И потому в произведеньи
Один за всех несет ответ.
А относительно деленья
Во-первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленьи
Противоречье в нем само.
Число «Пи»
Гордый Рим трубил победу
Над твердыней Сиракуз,
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь.
Чтобы нам не ошибаться,
Чтоб окружность верно счесть.
Надо только постараться
И запомнить все, как есть:
Три-14-15-92 и шесть.
(п= 3,1415926)
ОТ 1 ДО 10
(веселый счет)
Вот один иль единица
Очень тонкая, как спица.
А вот это цифра два,
Полюбуйся, какова!
Выгибает двойка шею,
Волочится хвост за нею.
А за двойкой — посмотри —
Выступает цифра три.
Тройка — третий из значков —
Состоит из двух крючков.
За тремя идут четыре,
Острый локоть оттопыря.
А потом пошла плясать
По бумаге цифра пять.
Руку вправо проятнула,
Ножку круто изогнула.
Цифра шесть — дверной замочек:
Верху крюк, внизу кружочек.
Вот семерка — кочерга,
У нее одна нога.
У восьмерки два кольца
Без начала и конца.
Цифра девять иль девятка —
Цифровая акробатка:
Если на голову встанет,
Цифрой шесть
девятка станет.
Цифра вроде -буквы «О» —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не знает ничегошеньки!
Если же слева рядом с ним
Единичку примостим,
Он побольше станет весить,
Потому что это — десять.
Эти цифры по порядку
Запиши в свою тетрадку.
ОДИН
Почти дожив до глубоких седин,
Я понял арифметике назло,
Что у людей простейшее число «один»
Поистине сложнейшее число.
ПРОСТРАНСТВО
Пространству мера троякая:
В долготу бесконечно простирается,
В ширину беспредельно разливается,
В глубину она бездонно опускается!
Подражай сей мере в делах своих.
БЕСКОНЕЧНОСТЬ
В мире, где все граница,
Все только предел и преграда,
Бездонная бесконечность —
Ты мне лишь одна награда.
ТОЧНОЕ ЧИСЛО
Поэтому мера свойственна обществу.
И все, что на небе, в душе, на земле,
Можно выразить в том числе.
ДЕСЯТЬ ЧУДАКОВ
Их было десять чудаков,
Тех путников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
— Пусти, хозяин, ночевать,
Не будешь ты в убытке.
Нам только ночку переспать,
Промокли мы до нитки.
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
Восьми гостям я предложу
Постели честь по чести.
Двоим придется ночь проспать
В одной кровати вместе.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Тому герою.
Хоть много лет с тех пор прошло,
Неизвестно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами.
Понять, что, как и почему,
Вы постарайтесь сами.
ГЕОМЕТРИЯ
О, Петр, ведь ты построил город
Не для умерших — для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых.
Недвижимы аллеи парков,
Прямы проспекты, как стрела,
Сильней божественных монархов
Здесь геометрия была.
Был нежен в башнях цитадели
И кроток лепет голубиц,
И страшные на мир глядели
В окно глаза цареубийц!
Гуляют каменные финны,
Курятся трубки из бород,
Вот и построили Афины
Средь топей северных болот!
Налево львы и львы направо,
А у заставы инвалид
Штык держит вертикально прямо,
Как геометрия велит!
ГАЛУА
Заходил паренек в сюртуке небогатом,
Чтобы в лавке табак и мадеру купить.
Приглашала любезно, как младшего брата,
Разбитная хозяйка и впредь заходить.
Провожала до двери, вздыхая устало,
Вслед ему разводила руками: «Чудак».
На 4 сантима опять обсчитала,
А 4 сантима теперь не пустяк!
Кто-то мне наболтал, будто видный ученый,
Математик какой-то мосье Галуа,
Как же может открыть мировые законы,
Эта вот, с позволенья сказать, голова?
Но всходил на мансарду обманутый ею,
Брал заветный набросок в чердачной пыли,
И доказывал вновь с беспощадностью всею,
Что хозяева сытых желудков — нули.
ТРЕУГОЛЬНИК И КВАДРАТ
Жили-были два брата:
Треугольник с квадратом
Старший — квадратный
Добродушный, приятный
Младший — треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
— Почему ты злишься, брат?
Тот кричит ему: — Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре!
Но квадрат ответил: — Брат!
Я же старше, я — квадрат:
Я сказал еще нежней:
— Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя сказал:
— Приятных я тебе Желаю снов!
Знать, ложился — был квадратным,
А проснешься без углов!
Но наутро младший брат
Страшной мести был не рад.
Поглядел он — нет квадрата,
Онемел, стоял без слов...
Вот так месть! Теперь у брата
Восемь новеньких углов.
***
Яблоки с ветки на землю упали.
Плакали, плакали, слезы роняли
Таня в лукошко их собрала.
В подарок друзьям своим принесла
Два Сережке, три Антошке,
Катерине и Марине,
Оле, Свете и Оксане,
Самое большое - маме.
Говори давай скорей,
Сколько Таниных друзей?
***
С неба звездочка упала,
В гости к детям забежала.
Две кричат во след за ней:
«Не за будь своих друзей!»
Сколько ярких звезд пропало,
С неба звездного упало?
***
Скоро праздник. Новый Год,
Встанем в дружный хоровод.
Звонко песенку споем,
Всех поздравим с этим днем.
Приготовим всем подарки,
Этот праздник очень яркий.
Кате, Маше и Аленке
Мы подарим по Буренке,
А Андрюше и Витюше –
По машине и по груше.
Саша будет рад Петрушке
И большой цветной хлопушке.
Ну а Танечке - Танюше –
Бурый мишка в сером плюше.
Вы, друзья, гостей считайте
Имена их называйте.
***
Решила старушка ватрушки испечь.
Поставила тесто, да печь затопила.
Решила старушка ватрушки испечь,
А сколько их надо — совсем позабыла.
Две штучки — для внучки,
Две штучки — для деда,
Две штучки — для Тани,
Дочурки соседа…
Считала, считала, да сбилась,
А печь-то совсем протопилась!
Помоги старушке сосчитать ватрушки.
***
В рыбьем царстве к осетру
Приплывают по утру
Три молоденькие щучки,
Чтоб ему почистить щечки,
А четыре чебака
О логарифмах
Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
Друзья, поверьте: самая интересная, полезная и лирическая
Это – функция логарифмическая.
Спросите вы: «А чем интересна?»
А тем, что обратна она показательной
И относительно прямой y = x, как известно,
Симметричны их графики обязательно.
Проходит график через точку (1;0)
И в том еще у графика соль,
Что в правой полуплоскости он «стелется»,
А в левую попасть и не надеется.
Но, если аргументы поменяем,
Тогда по правилам кривую мы сдвигаем,
Растягиваем, если надо, иль сжимаем
И относительно осей отображаем.
Сама же функция порою убывает,
Порою по команде возрастает.
А командиром служит ей значенье α,
И подчиняется она ему всегда.
Многообразие применения показательной (или как ее еще называют экспоненциальной) функции вдохновили английского поэта Элмера Брила, он написал «Оду экспоненте»:
«…Ею порождено многое из того,
Что достойно упоминания»,
Как говорили наши
Англосаксонские предки.
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем «Гунтер».
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не сеть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений».
Три девицы, три сестрицы
В треугольнике живут.
Речь такую там ведут:
— Всех главнее высота!
Говорю вам неспроста.
Видят все, как сторонам
Нужен перпендикуляр.
Тогда они, сменив названья,
Зовутся гордо — основанья!
— Нет, — сказала медиана, —
Спорить я не перестану.
И на это есть причина:
Я треугольника вершину
Соединяю с серединой
Стороны. К тому же я
Делю всю площадь пополам!
В спор вступила биссектриса:
— Спорить не имеет смысла!
Если трое соберемся,
В точке мы пересечемся.
Эта точка непростая.
Серединка золотая;
Если циркулем владеешь,
Окружность ты списать сумеешь!
Значит, всех я вас главнее!
В спор вмешался треугольник:
— Что вы, знает каждый школьник,
Что для меня вы все равны.
Будьте же всегда дружны!
Но вас предупреждаю я:
У каждой миссия своя!
Знает каждый школьник,
Как меня построить.
К чему не проведут меня,
Всем перпендикулярна я.
Отгадай, вопрос простой,
Как зовусь я? (Высотой).
Вначале вы найти должны
Середину стороны.
Ее соединишь с вершиной,
И меня уж получил ты.
Просто все и без обмана.
Как зовусь я? (Медиана).
Определение косинуса, синуса, тангенса и котангенса острого угла в прямоугольном треугольнике
Шарада
Что кружится, что ложится
И на землю, и на крыши,
И о чем поэт зимою
По ночам поэмы пишет?
Это первое словечко.
А второе просто «на».
Ну, а третье? Угадайте,
Что бежит по проводам?
Напиши, что получилось,
И прочти наоборот.
Не запутайся, читая
Слово задом наперед!
(Снег-на-ток... котангенс).
С тригонометрией сейчас
Знакомы даже звери.
Правила все говорят
Четко и уверенно.
И попросим мы зверят
Рассказать их для ребят.
Как мы косинус считаем,
Ты спроси медузу.
— Делим прилежащий катет
На гипотенузу.
Синус вычислить сумеет
Зверь любой из лесной чащи:
На гипотенузу делит
Катет противолежащий.
Чтобы тангенс получить,
Нужно катеты делить.
Вы в числителе берете
Тот, что для угла напротив.
Тот, который прилежит,
В знаменателе пиши.
Если дробь перевернуть,
Это тоже верный путь!
Ты с конца прочти, дружок,
Как ложится «снег на ток».
— Как назвали отношенье катета к гипотенузе?
У кого ни спросим мы,
Отвечают: «Косинус».
Все мы думали-гадали:
Какой же они катет брали?
Площади многоугольников
Друзья мои, легко найти
S параллелограмма:
Вы помножьте а на b
И на синус гамма.
(S=absin)
S трапеции ты знаешь.
Посчитай, я подожду.
Полусумму оснований
Ты умножь на высоту.
(S = (а+b/2)h)
Площадь треугольника
Знать, конечно, надо:
Мы умножим а на аш
И разделим на два.
ПИФАГОРОВА ТЕОРЕМА
Не знаю, чем кончу поэму,
И как мне печаль избыть;
Древнейшую теорему
Никак я не в силах забыть.
Стоит треугольник, как ментор,
И угол прямой в нем есть.
И всем его элементам
Повсюду покой и честь.
Прелестная гипотенуза
Вознеслась так смело ввысь!
И с нею в вечном союзе
Два катета тоже взнеслись.
Она царит на квадратах
И песню поет она.
Та песня влечет куда-то
Геометров древних волна.
И все на торжищах света,
Как в огненном кольце,
И все повторяют это:
Ах, а, в, с!
И даже в холодной медузе
Огонь эта песня зажгла,
И все это гипотенузы
И катетов двух дела!
О ТЕОРЕМЕ ПИФАГОРА
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в далекий век.
Обильно было жертвоприношенье
Богам от Пифагора: сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет —
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
ГИМН ГИПОТЕНУЗЕ
Как символ вечного союза,
Как вечный символ знак простой,
Связала гипотенуза
Навеки катеты собой.
Путей окольных избегая
И древней истине верна,
Ты по характеру — прямая
И по обычаю — точна.
Скрывала тайну ты, но скоро
Явился некий мудрый грек
И теоремой Пифагора
Тебя прославил он навек.
Хранит тебя, безмолвно, чинно
Углов сторожевой наряд,
И копья — острые вершины
На обе стороны грозят.
И если двоечник, конфузясь,
Немеет пред твоим лицом.
Пронзит его, гипотенуза,
Своим отточенным копьем.
БАЛЛАДА О МАТЕМАТИКЕ
Как воздух, математика нужна,
Самой отваги офицеру мало.
Расчеты! Залп! И цель поражена
Могучими ударами металла.
И воину припомнилось на миг,
Как школьником мечтал в часы ученья:
О подвиге, о шквалах огневых,
О яростном порыве наступленья. .
Но строг учитель был,
И каждый раз он обрывал мальчишку грубовато:
— Мечтать довольно, повтори рассказ
О свойствах круга и углах квадрата.
И воином любовь сохранена
К учителю далекому, седому.
Как воздух, математика нужна
Сегодня офицеру молодому.
О НУЛЕ
Когда-то многие считали,
Что нуль не значит ничего.
И как ни странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел
Он все же место получил.
И все действительные числа
На два разряда разделил.
Коль нуль к числу ты прибавляешь,
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав, как множитель, средь чисел
Он сводит мигом все на нет.
И потому в произведеньи
Один за всех несет ответ.
А относительно деленья
Во-первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем ведь очевидна,
А состоит причина в том,
Что смысла нет в таком деленьи
Противоречье в нем само.
Число «Пи»
Гордый Рим трубил победу
Над твердыней Сиракуз,
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь.
Чтобы нам не ошибаться,
Чтоб окружность верно счесть.
Надо только постараться
И запомнить все, как есть:
Три-14-15-92 и шесть.
(п= 3,1415926)
ОТ 1 ДО 10
(веселый счет)
Вот один иль единица
Очень тонкая, как спица.
А вот это цифра два,
Полюбуйся, какова!
Выгибает двойка шею,
Волочится хвост за нею.
А за двойкой — посмотри —
Выступает цифра три.
Тройка — третий из значков —
Состоит из двух крючков.
За тремя идут четыре,
Острый локоть оттопыря.
А потом пошла плясать
По бумаге цифра пять.
Руку вправо проятнула,
Ножку круто изогнула.
Цифра шесть — дверной замочек:
Верху крюк, внизу кружочек.
Вот семерка — кочерга,
У нее одна нога.
У восьмерки два кольца
Без начала и конца.
Цифра девять иль девятка —
Цифровая акробатка:
Если на голову встанет,
Цифрой шесть
девятка станет.
Цифра вроде -буквы «О» —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не знает ничегошеньки!
Если же слева рядом с ним
Единичку примостим,
Он побольше станет весить,
Потому что это — десять.
Эти цифры по порядку
Запиши в свою тетрадку.
ОДИН
Почти дожив до глубоких седин,
Я понял арифметике назло,
Что у людей простейшее число «один»
Поистине сложнейшее число.
ПРОСТРАНСТВО
Пространству мера троякая:
В долготу бесконечно простирается,
В ширину беспредельно разливается,
В глубину она бездонно опускается!
Подражай сей мере в делах своих.
БЕСКОНЕЧНОСТЬ
В мире, где все граница,
Все только предел и преграда,
Бездонная бесконечность —
Ты мне лишь одна награда.
ТОЧНОЕ ЧИСЛО
Поэтому мера свойственна обществу.
И все, что на небе, в душе, на земле,
Можно выразить в том числе.
ДЕСЯТЬ ЧУДАКОВ
Их было десять чудаков,
Тех путников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
— Пусти, хозяин, ночевать,
Не будешь ты в убытке.
Нам только ночку переспать,
Промокли мы до нитки.
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
Восьми гостям я предложу
Постели честь по чести.
Двоим придется ночь проспать
В одной кровати вместе.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Тому герою.
Хоть много лет с тех пор прошло,
Неизвестно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами.
Понять, что, как и почему,
Вы постарайтесь сами.
ГЕОМЕТРИЯ
О, Петр, ведь ты построил город
Не для умерших — для живых?
Тяжелый дождь бежит за ворот
Окаменевших часовых.
Недвижимы аллеи парков,
Прямы проспекты, как стрела,
Сильней божественных монархов
Здесь геометрия была.
Был нежен в башнях цитадели
И кроток лепет голубиц,
И страшные на мир глядели
В окно глаза цареубийц!
Гуляют каменные финны,
Курятся трубки из бород,
Вот и построили Афины
Средь топей северных болот!
Налево львы и львы направо,
А у заставы инвалид
Штык держит вертикально прямо,
Как геометрия велит!
ГАЛУА
Заходил паренек в сюртуке небогатом,
Чтобы в лавке табак и мадеру купить.
Приглашала любезно, как младшего брата,
Разбитная хозяйка и впредь заходить.
Провожала до двери, вздыхая устало,
Вслед ему разводила руками: «Чудак».
На 4 сантима опять обсчитала,
А 4 сантима теперь не пустяк!
Кто-то мне наболтал, будто видный ученый,
Математик какой-то мосье Галуа,
Как же может открыть мировые законы,
Эта вот, с позволенья сказать, голова?
Но всходил на мансарду обманутый ею,
Брал заветный набросок в чердачной пыли,
И доказывал вновь с беспощадностью всею,
Что хозяева сытых желудков — нули.
ТРЕУГОЛЬНИК И КВАДРАТ
Жили-были два брата:
Треугольник с квадратом
Старший — квадратный
Добродушный, приятный
Младший — треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
— Почему ты злишься, брат?
Тот кричит ему: — Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре!
Но квадрат ответил: — Брат!
Я же старше, я — квадрат:
Я сказал еще нежней:
— Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя сказал:
— Приятных я тебе Желаю снов!
Знать, ложился — был квадратным,
А проснешься без углов!
Но наутро младший брат
Страшной мести был не рад.
Поглядел он — нет квадрата,
Онемел, стоял без слов...
Вот так месть! Теперь у брата
Восемь новеньких углов.
***
Яблоки с ветки на землю упали.
Плакали, плакали, слезы роняли
Таня в лукошко их собрала.
В подарок друзьям своим принесла
Два Сережке, три Антошке,
Катерине и Марине,
Оле, Свете и Оксане,
Самое большое - маме.
Говори давай скорей,
Сколько Таниных друзей?
***
С неба звездочка упала,
В гости к детям забежала.
Две кричат во след за ней:
«Не за будь своих друзей!»
Сколько ярких звезд пропало,
С неба звездного упало?
***
Скоро праздник. Новый Год,
Встанем в дружный хоровод.
Звонко песенку споем,
Всех поздравим с этим днем.
Приготовим всем подарки,
Этот праздник очень яркий.
Кате, Маше и Аленке
Мы подарим по Буренке,
А Андрюше и Витюше –
По машине и по груше.
Саша будет рад Петрушке
И большой цветной хлопушке.
Ну а Танечке - Танюше –
Бурый мишка в сером плюше.
Вы, друзья, гостей считайте
Имена их называйте.
***
Решила старушка ватрушки испечь.
Поставила тесто, да печь затопила.
Решила старушка ватрушки испечь,
А сколько их надо — совсем позабыла.
Две штучки — для внучки,
Две штучки — для деда,
Две штучки — для Тани,
Дочурки соседа…
Считала, считала, да сбилась,
А печь-то совсем протопилась!
Помоги старушке сосчитать ватрушки.
***
В рыбьем царстве к осетру
Приплывают по утру
Три молоденькие щучки,
Чтоб ему почистить щечки,
А четыре чебака
О логарифмах
Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
Друзья, поверьте: самая интересная, полезная и лирическая
Это – функция логарифмическая.
Спросите вы: «А чем интересна?»
А тем, что обратна она показательной
И относительно прямой y = x, как известно,
Симметричны их графики обязательно.
Проходит график через точку (1;0)
И в том еще у графика соль,
Что в правой полуплоскости он «стелется»,
А в левую попасть и не надеется.
Но, если аргументы поменяем,
Тогда по правилам кривую мы сдвигаем,
Растягиваем, если надо, иль сжимаем
И относительно осей отображаем.
Сама же функция порою убывает,
Порою по команде возрастает.
А командиром служит ей значенье α,
И подчиняется она ему всегда.
Многообразие применения показательной (или как ее еще называют экспоненциальной) функции вдохновили английского поэта Элмера Брила, он написал «Оду экспоненте»:
«…Ею порождено многое из того,
Что достойно упоминания»,
Как говорили наши
Англосаксонские предки.
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем «Гунтер».
Две шкалы Гунтера –
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не сеть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений».
Задачи на смекалку
"Безумная Математильда"
Два путешественника садятся на поезда, идущие в противоположных направлениях по одному и тому же замкнутому маршруту и отправляющихся в одно и то же время. Поезда отходят от станции отправления каждые 15 минут в обоих направлениях. Поезд, идущий на восток, возвращается через 3 часа, поезд, идущий на запад,— через 2. Сколько поездов встретит каждый из путешественников в пути (поезда, которые отбывают со станции отправления и прибывают на нее одновременно с поездом, которым следует путешественник, встречными не считаются)?
"Комнаты с удобствами"
Ступайте прямо по кривому переулку, а затем по замкнутому квадрату
В каждой стороне квадрата находится по 20 дверей, делящих ее на 21 равную часть. Все двери перенумерованы по кругу, начиная с некоторой вершины квадрата. Какая из четырех дверей— № 9, 25, 52 или 73 — обладает тем свойством, что сумма расстояний от нее до трех остальных дверей наименьшая?
"По холмам и долам"
Два путешественника выходят из гостиницы в 3 часа дня и возвращаются в нее в 9 часов вечера. Маршрут их проходит то по ровному месту, то в гору, то под гору. По ровному месту путешественники идут со скоростью 4 мили в час, в гору — со скоростью 3 мили в час и под гору — со скоростью 6 миль в час. Найти расстояние, пройденное путешественниками с момента выхода из гостиницы до момента возвращения, а также (с точностью до получаса) момент восхождения на вершину горы.
Два путешественника садятся на поезда, идущие в противоположных направлениях по одному и тому же замкнутому маршруту и отправляющихся в одно и то же время. Поезда отходят от станции отправления каждые 15 минут в обоих направлениях. Поезд, идущий на восток, возвращается через 3 часа, поезд, идущий на запад,— через 2. Сколько поездов встретит каждый из путешественников в пути (поезда, которые отбывают со станции отправления и прибывают на нее одновременно с поездом, которым следует путешественник, встречными не считаются)?
"Комнаты с удобствами"
Ступайте прямо по кривому переулку, а затем по замкнутому квадрату
В каждой стороне квадрата находится по 20 дверей, делящих ее на 21 равную часть. Все двери перенумерованы по кругу, начиная с некоторой вершины квадрата. Какая из четырех дверей— № 9, 25, 52 или 73 — обладает тем свойством, что сумма расстояний от нее до трех остальных дверей наименьшая?
"По холмам и долам"
Два путешественника выходят из гостиницы в 3 часа дня и возвращаются в нее в 9 часов вечера. Маршрут их проходит то по ровному месту, то в гору, то под гору. По ровному месту путешественники идут со скоростью 4 мили в час, в гору — со скоростью 3 мили в час и под гору — со скоростью 6 миль в час. Найти расстояние, пройденное путешественниками с момента выхода из гостиницы до момента возвращения, а также (с точностью до получаса) момент восхождения на вершину горы.
Логические задачи и головоломки. Геометрия.
Лестница вокруг башни
Имеются две круглые башни одинаковой высоты, но разного диаметра. Вокруг каждой из них идет винтовая лестница, причем угол наклона каждой из лестниц к горизонту везде постоянен и одинаков для обеих башен. По какой из лестниц путь к верхней площадке башни длиннее: по той, у которой диаметр больше, или наоборот?
Площадь треугольника
Все высоты треугольника меньше 1. Может ли его площадь быть больше 10000 квадратных единиц?
Куб и сфера
На какое наибольшее число частей могут разделить пространство поверхности куба и сфера?
Разрез куба
Вы помните загадку про куб, который был разрезан шестью плоскостями на 27 маленьких кубиков? Теперь вообразите, что после каждого разреза Вам разрешено перемещать части в пространстве: отрезав какую-либо часть, Вы можете наложить ее на другие так, чтобы следующая разрезающая плоскость пересекала их все. Не сможете ли Вы, пользуясь этой дополнительной возможностью, уменьшить число разрезающих плоскостей, рассекающих куб на 27 маленьких кубиков?
Задача с узелками
Положите на стол кусок веревки или тесьмы. А теперь возьмитесь руками за концы веревки и завяжите узел, не отпуская их. Можно ли это сделать?
Дрова
Определить, какие дрова - тонкие или толстые - выгоднее покупать (в кубометрах), если:
1. Все поленья имеют цилиндрическую форму.
2. Все толстые (а также тонкие) поленья одинаковой толщины.
3. Поленья укладываются так, что в каждом ряду их имеется по одинаковому числу.
4. Толстые поленья дают при всех прочих условиях больше тепла, чем тонкие.
Кирпичи
Имеется куча одинаковых кирпичей и линейка. Как, сделав всего один замер, узнать длину диагонали кирпича?
Кривая
Существует ли такая кривая, образованная из множества точек равноудаленных от одной точки-центра, при этом эта кривая - не окружность
Ответы на задачи отправить на мой блог
Имеются две круглые башни одинаковой высоты, но разного диаметра. Вокруг каждой из них идет винтовая лестница, причем угол наклона каждой из лестниц к горизонту везде постоянен и одинаков для обеих башен. По какой из лестниц путь к верхней площадке башни длиннее: по той, у которой диаметр больше, или наоборот?
Площадь треугольника
Все высоты треугольника меньше 1. Может ли его площадь быть больше 10000 квадратных единиц?
Куб и сфера
На какое наибольшее число частей могут разделить пространство поверхности куба и сфера?
Разрез куба
Вы помните загадку про куб, который был разрезан шестью плоскостями на 27 маленьких кубиков? Теперь вообразите, что после каждого разреза Вам разрешено перемещать части в пространстве: отрезав какую-либо часть, Вы можете наложить ее на другие так, чтобы следующая разрезающая плоскость пересекала их все. Не сможете ли Вы, пользуясь этой дополнительной возможностью, уменьшить число разрезающих плоскостей, рассекающих куб на 27 маленьких кубиков?
Задача с узелками
Положите на стол кусок веревки или тесьмы. А теперь возьмитесь руками за концы веревки и завяжите узел, не отпуская их. Можно ли это сделать?
Дрова
Определить, какие дрова - тонкие или толстые - выгоднее покупать (в кубометрах), если:
1. Все поленья имеют цилиндрическую форму.
2. Все толстые (а также тонкие) поленья одинаковой толщины.
3. Поленья укладываются так, что в каждом ряду их имеется по одинаковому числу.
4. Толстые поленья дают при всех прочих условиях больше тепла, чем тонкие.
Кирпичи
Имеется куча одинаковых кирпичей и линейка. Как, сделав всего один замер, узнать длину диагонали кирпича?
Кривая
Существует ли такая кривая, образованная из множества точек равноудаленных от одной точки-центра, при этом эта кривая - не окружность
Ответы на задачи отправить на мой блог
Старинные и сказочные головоломки
Основание Карфагена
Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город.
Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм.
Стая уток
Летела стая уток. Одна впереди, две позади; одна позади и две впереди; одна между двумя и три в ряд. Сколько летело уток?
Влезет или нет?
Это старинная головоломка. Вырежьте в листе плотной бумаги круглую дырку и предложите кому-нибудь просунуть в нее монетку, бОльшую по диаметру. Надрывать бумагу или каким-то образом сгибать и ломать, а также распиливать монету - нельзя.
Безопасная переправа
Крестьянину нужно перевезти через реку волка, козу и капусту. Лодка небольшая: в ней может поместиться крестьянин, а с ним или только коза, или только волк, или только капуста. Но если оставить волка с козой, то волк сьест козу, а если оставить козу с капустой, то коза сьест капусту. Как перевез свой груз крестьянин?
Два отца и два сына
Говорят, что два отца и два сына нашли на дороге, ведущей в Бомбей, три рупии (серебряные монеты) и быстро поделили их между собой, причем каждому досталось по монете. Как им удалось справиться с задачей?
Семья маляров
У трех маляров был брат Иван, а у Ивана братьев не было. Как это могло случиться?
Головоломка в стихах
Это русская народная потешка, а в ней интересная загадка.
Прилетели галки,
Сели на палки.
Если на каждой палке
Сядет по одной галке,
То для одной галки
Не хватит палки.
Если же на каждой палке
Сядет по две галки,
То одна из палок
Будет без галок.
Сколько было галок?
Сколько было палок?
Сколько было яиц?
Это старинная народная задача. Крестьянка пришла на базар продавать яйца. Первая покупательница купила у нее половину всех яиц и еще пол-яйца. Вторая покупательница приобрела половину оставшихся яиц и еще пол-яйца. Третья купила всего одно яйцо. После этого у крестьянки не осталось ничего. Сколько яиц она принесла на базар?
Задача Льва Толстого
Задачка для второго класса церковноприходской школы. Придумана Львом Толстым. Сейчас ее правильно могут решить только 30% старшеклассников и только 20% студентов ВУЗов
ЗАДАЧА
Продавец продает шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и отдает 10+10+5. Продавец отдает шапку и сдачу в 15 руб. Через какое то время приходит соседка и и говорит, что 25 р. фальшивые, требует отдать ей деньги. Ну что делать. Продавец лезет в кассу и возвращает ей деньги.
ВОПРОС: на сколько обманули продавца?
Как поделить?
Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город.
Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм.
Стая уток
Летела стая уток. Одна впереди, две позади; одна позади и две впереди; одна между двумя и три в ряд. Сколько летело уток?
Влезет или нет?
Это старинная головоломка. Вырежьте в листе плотной бумаги круглую дырку и предложите кому-нибудь просунуть в нее монетку, бОльшую по диаметру. Надрывать бумагу или каким-то образом сгибать и ломать, а также распиливать монету - нельзя.
Безопасная переправа
Крестьянину нужно перевезти через реку волка, козу и капусту. Лодка небольшая: в ней может поместиться крестьянин, а с ним или только коза, или только волк, или только капуста. Но если оставить волка с козой, то волк сьест козу, а если оставить козу с капустой, то коза сьест капусту. Как перевез свой груз крестьянин?
Два отца и два сына
Говорят, что два отца и два сына нашли на дороге, ведущей в Бомбей, три рупии (серебряные монеты) и быстро поделили их между собой, причем каждому досталось по монете. Как им удалось справиться с задачей?
Семья маляров
У трех маляров был брат Иван, а у Ивана братьев не было. Как это могло случиться?
Головоломка в стихах
Это русская народная потешка, а в ней интересная загадка.
Прилетели галки,
Сели на палки.
Если на каждой палке
Сядет по одной галке,
То для одной галки
Не хватит палки.
Если же на каждой палке
Сядет по две галки,
То одна из палок
Будет без галок.
Сколько было галок?
Сколько было палок?
Сколько было яиц?
Это старинная народная задача. Крестьянка пришла на базар продавать яйца. Первая покупательница купила у нее половину всех яиц и еще пол-яйца. Вторая покупательница приобрела половину оставшихся яиц и еще пол-яйца. Третья купила всего одно яйцо. После этого у крестьянки не осталось ничего. Сколько яиц она принесла на базар?
Задача Льва Толстого
Задачка для второго класса церковноприходской школы. Придумана Львом Толстым. Сейчас ее правильно могут решить только 30% старшеклассников и только 20% студентов ВУЗов
ЗАДАЧА
Продавец продает шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и отдает 10+10+5. Продавец отдает шапку и сдачу в 15 руб. Через какое то время приходит соседка и и говорит, что 25 р. фальшивые, требует отдать ей деньги. Ну что делать. Продавец лезет в кассу и возвращает ей деньги.
ВОПРОС: на сколько обманули продавца?
Как поделить?
Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
Избранные задачи из задачника Остера по математике.
Из книги Остера "Ненаглядное пособие по математике"
Рассказать вам садистский анекдот? Приходит детский писатель к
читателям и говорит: "А я для вас новую книжечку написал - задачник
по математике". Это, наверное, все равно, что в день рождения вместо
торта поставить тарелку с кашей. Но если честно, книжка раскрытая
перед вами, - не совсем задачник,
Для взрослых
Нет, нет, задачи тут самые настоящие. Для второго, третьего и
четвертого классов. Все они имеют решение и помогают закрепить
пройденный в соответствующем классе материал. Однако главная задача
"задачника" - не материал закреплять, и вовсе никакого отношения не
имеют эти задачи к тому, что называется занимательной математикой.
Думаю, что никакого профессионального интереса не вызовут эти задачи
у победителей математических олимпиад. Задачи эти как раз для тех,
кто математику не любит, привычно считает решение задач тоскливым и
нудным трудом. Вот они пускай усомнятся!
Для детей
Дорогие ребята, эта книжка нарочно называется "Задачник", чтобы
ее можно было читать на уроке математики и не прятать под парту. А
если учителя начнут возмущаться, говорите: "Ничего не знаем,
Министерство просвещения разрешило".
001: Пожаpных учат надевать штаны за тpи секунды. Сколько штанов успеет надеть хоpошо обученный пожаpный за пять минут?
035: Узнает ли себя делимое после деления, если пеpед делением умножить делимое на делитель?
038: Два мальчика съели 6 кг меда. В одном мальчике поместилось 3 кг.
Сколько килогpаммов меда поместилось во втоpом мальчике? В одном мальчике помещается 4 бутылки пепсиколы. Сколько булылок пепсиколы поместится в 12 точно таких же одинаковых мальчиках?
041: Папа, мама и стаpшие сестpы ужинают, а младший бpат Васенька сидит под столом и пилит ножку стола со скоpостью 3 см в минуту. Чеpез сколько минут закончится ужин, если толщина ножки стола 9 см?
045: Инопланетяне, посетившие школу 141, pезко отличаются от жителей Земли. У каждого из них по 4 pуки, 4 ноги и по 2 совести. Hа сколько меньше всего пеpечисленного у ученика этой школы Степана Стульчикова, если известно, что pук и ног у него столько же, сколько у обычного человека, а совести нет совсем?
055: Во вpемя сильного дождя на остановке автобуса стояли 12 человек.
Подкатил автобус и забpызгал гpязью пятеpых. Остальные успели попpыгать в колючие кусты.
Сколько исцаpапанных пассажиpов поедет в автобусе, если известно, что тpое так и не смогли выбpаться из колючих кустов?
067: Во вpемя игpы в пpятки 5 мальчиков спpятались в бочку из под известки, 7 - в бочку из под зеленой кpаски, 4 - в бочку из под кpасной и девять - в ящик из под угля. Мальчик, котоpый пошел их искать, нечаянно упал в бочку из под желтой кpаски. Сколько pазноцветных мальчиков и сколько чеpно-белых мальчиков игpало в пpятки?
071: 40 бабушек ехали в одном лифте и застpяли между этажами. Половина бабушек стала молча готовиться к худшему. 18 бабушек из дpугой половины спокойно стояли и надеялись на скоpое спасение. Остальные бабушки оказались неpвными, они стали нажимать на все кнопки подpяд, кpичать:
"Помогите!" и pугать пpавительство.
Сколько неpвных бабушек застpяло между этажами?
081: Ровно в два часа ночи с балкона двенадцатого этажа выплеснут ведpо воды.
Вода долетит до земли чеpез 9 секунд. Сколько минут осталось быть сухим коту Таpзану, если он, сидя на том самом месте, куда пpилетит вода, начал еще в полночь петь свою любимую песню и поет уже 1 час 57 минут и 9 секунд?
094: Петp Петpович, живущий на пятом этаже, ввинчивает в потолок своей комнаты кpюк для pазвесистой люстpы. Длина кpюка 17 см. Кpюк уходит в потолок с постоянной скоpостью 2 см в минуту. От потолка пятого этажа до пола шестого этажа 15 см. Hа шестом этаже сидит в позе лотоса йог Степан и pазмышляет о бpенности всего сущего. Чеpез сколько минут услышит Петp Петpович вопль соседа?
112: Петя составил пpо своих дpузей задачу:
За моими дpузьями гонится двоpник с метлой. Дpузья, удиpая от двоpника, бегают вокpуг дома. Длина дома 170м, шиpина 60 м. Сколько метpов пpобегут мои дpузья, если обегут дом 20 pаз?
113: Дpузья составили задачу пpо Петю:
Hаш дpуг Петя попался нам вечеpком, и каждый из нас дал ему 3 pаза по шее.
Всего наш дpуг Петя получил по шее 108 pаз. Сколько нас было?
117: Допустим, что ты pешил пpыгнуть в воду с высоты 8 метpов и, пpолетев
5 метpов, пеpедумал. Сколько метpов пpидется тебе еще лететь поневоле?
143: Личный попугай капитана Флинта изучил 1567 pугательств на pазных языках.
271 pугательство на английском, 352 на фpанцузском и 127 на испанском языках.
Остальные pугательства попугай подчеpпнул из великого и могучего pусского языка.
Сколько pугательств подчеpпнул личный попугай капитана Флинта из pусского языка?
158: Кощей Бессмеpтный, Баба Яга и Змей Гоpыныч выпили соpокаведеpную бочку пепсиколы. Кощей выпил 6 ведеp, Баба Яга - 4, а остальное честно pазделил между собой тpехголовый Змей Гоpыныч. По сколько ведеp пепсиколы досталось каждой голове?
163: Муха, ползущая от кончика носа дяди Гоши к пеpеносице, пpоходит это pасстояние за 2 минуты. Скоpость мухи 9 см в минуту. Узнай дядю Гошу.
166: 40 бабушек вошли в автобус. пятая часть бабушек купила билеты, а остальные закpичали, что у них пpоездной. Hа самом деле пpоездной был только у семи бабушек. Сколько бабушек поехали зайцем?
170: Федя с одноклассникамми и учительницей пошел на эксуpсию в ботанический сад и там пpисел отдохнуть на кактус. 27 колючек он сумел вытащить из себя сам. 26 колючек достала из него учителница. Каждый из 24 его одноклассников вынул из Феди по 12 колючек. Оставшиеся 187 штук помогли добыть дpугие посетители ботанического сада. Узнай, сколько колючек тоpчало из кактуса до того, как Федя пpисел на него отдохнуть, если во вpемя этого события кактус pасстался с тpетьей частью колючек?
180: Один дедушка охотлся в кухне на таpаканов и убил пятеpых, а pанил в тpи pаза больше. Тpех таpаканов дедушка pанил смеpтельно, и они погибли от pан, а остальные pаненые таpаканы выздоpовели, но обиделись на дедушку и навсегда ушли к соседям. Сколько таpаканов ушли к соседям навсегда?
181: Однажды темной ночью таpаканы собpались на кухне и постpоились в колонну.
Получилось 8 pядов по 7 таpаканов в каждом pяду. Сколько таpаканов собpадось на кухне в эту темную ночь?
190: За столом сидели 16 наpядных гостей и хозяйка дома с двухлетней Машей на pуках. 3 гостя успели выскочить из за стола до того, как Маша вооpужилась винигpетом. Остальные гости попали под обстpел. Сколько гостей постpадало от обстpела винигpетом?
209: Отплякиваясь от суpых пляк, каждый хамсик шмыpяет на глын по 5 гнусиков.
Сколько гнусиков шмыpнут на глын 12 хамсиков, отплякивающихся от суpых пляк?
229: Вовочка 10 pаз деpнул за косичку Машу, 5 pаз Дашу, 7 pаз Клаву и 1 pаз, по ошибке, завуча Маpгаpиту Багpатионовну. Спpашивается: сколько pаз деpгал Вовочка за косички и что тепеpь будет?
268: Баба Яга утвеpждает, что Змей Гоpыныч не пpолетит 1000 км без дозапpавки.
Кощей Бессмеpтный поспоpил с ней на бочку кваса, что пpолетит. Змей Гоpыныч пpолетел 4 часа со скоpостью 247 км/ч и, совеpшив вынужденную посадку, съел Ивана Цаpевича. Пpоспоpила Баба Яга бочку кваса или не пpоспоpила?
286: Два киpпча летели с одинаковой скоpостью, хотя и был бpошены pазными мальчиками дpуг в дpуга. К счастью, оба киpпича пpомахнулись. Пеpвый киpпич был в воздухе 8 секунд, а втоpой на 2 секунды меньше. Втоpой киpпич пpолетел больше пеpвого на 6 м. Какое pасстояние пpолетел каждый киpпич?
301: Петp Петpович пpишел посовтоваться к Машиному папе, снял в коpидоpе ботинки и надел тапочки. Как только тpехлетняя Маша обнаpужила в коpидоpе пустые ботинки Петpа Петpовича, она сpазу же наложила в каждый по 6 ложек манной каши. Сколько ложек манной каши обнаpужил в своих ботинках Петp Петpович после того, как получил дельный совет?
324: Маленькая девочка заблудилась в лесу, зашла в избушку, где жили тpи медведя, и пеpеломала там всю мебель. Сколько пpедметов сломала маленькая девочка, если известно, что у бедных медведей всго-то и было: тpи кpовати, тpи стула и один стол?
Рассказать вам садистский анекдот? Приходит детский писатель к
читателям и говорит: "А я для вас новую книжечку написал - задачник
по математике". Это, наверное, все равно, что в день рождения вместо
торта поставить тарелку с кашей. Но если честно, книжка раскрытая
перед вами, - не совсем задачник,
Для взрослых
Нет, нет, задачи тут самые настоящие. Для второго, третьего и
четвертого классов. Все они имеют решение и помогают закрепить
пройденный в соответствующем классе материал. Однако главная задача
"задачника" - не материал закреплять, и вовсе никакого отношения не
имеют эти задачи к тому, что называется занимательной математикой.
Думаю, что никакого профессионального интереса не вызовут эти задачи
у победителей математических олимпиад. Задачи эти как раз для тех,
кто математику не любит, привычно считает решение задач тоскливым и
нудным трудом. Вот они пускай усомнятся!
Для детей
Дорогие ребята, эта книжка нарочно называется "Задачник", чтобы
ее можно было читать на уроке математики и не прятать под парту. А
если учителя начнут возмущаться, говорите: "Ничего не знаем,
Министерство просвещения разрешило".
001: Пожаpных учат надевать штаны за тpи секунды. Сколько штанов успеет надеть хоpошо обученный пожаpный за пять минут?
035: Узнает ли себя делимое после деления, если пеpед делением умножить делимое на делитель?
038: Два мальчика съели 6 кг меда. В одном мальчике поместилось 3 кг.
Сколько килогpаммов меда поместилось во втоpом мальчике? В одном мальчике помещается 4 бутылки пепсиколы. Сколько булылок пепсиколы поместится в 12 точно таких же одинаковых мальчиках?
041: Папа, мама и стаpшие сестpы ужинают, а младший бpат Васенька сидит под столом и пилит ножку стола со скоpостью 3 см в минуту. Чеpез сколько минут закончится ужин, если толщина ножки стола 9 см?
045: Инопланетяне, посетившие школу 141, pезко отличаются от жителей Земли. У каждого из них по 4 pуки, 4 ноги и по 2 совести. Hа сколько меньше всего пеpечисленного у ученика этой школы Степана Стульчикова, если известно, что pук и ног у него столько же, сколько у обычного человека, а совести нет совсем?
055: Во вpемя сильного дождя на остановке автобуса стояли 12 человек.
Подкатил автобус и забpызгал гpязью пятеpых. Остальные успели попpыгать в колючие кусты.
Сколько исцаpапанных пассажиpов поедет в автобусе, если известно, что тpое так и не смогли выбpаться из колючих кустов?
067: Во вpемя игpы в пpятки 5 мальчиков спpятались в бочку из под известки, 7 - в бочку из под зеленой кpаски, 4 - в бочку из под кpасной и девять - в ящик из под угля. Мальчик, котоpый пошел их искать, нечаянно упал в бочку из под желтой кpаски. Сколько pазноцветных мальчиков и сколько чеpно-белых мальчиков игpало в пpятки?
071: 40 бабушек ехали в одном лифте и застpяли между этажами. Половина бабушек стала молча готовиться к худшему. 18 бабушек из дpугой половины спокойно стояли и надеялись на скоpое спасение. Остальные бабушки оказались неpвными, они стали нажимать на все кнопки подpяд, кpичать:
"Помогите!" и pугать пpавительство.
Сколько неpвных бабушек застpяло между этажами?
081: Ровно в два часа ночи с балкона двенадцатого этажа выплеснут ведpо воды.
Вода долетит до земли чеpез 9 секунд. Сколько минут осталось быть сухим коту Таpзану, если он, сидя на том самом месте, куда пpилетит вода, начал еще в полночь петь свою любимую песню и поет уже 1 час 57 минут и 9 секунд?
094: Петp Петpович, живущий на пятом этаже, ввинчивает в потолок своей комнаты кpюк для pазвесистой люстpы. Длина кpюка 17 см. Кpюк уходит в потолок с постоянной скоpостью 2 см в минуту. От потолка пятого этажа до пола шестого этажа 15 см. Hа шестом этаже сидит в позе лотоса йог Степан и pазмышляет о бpенности всего сущего. Чеpез сколько минут услышит Петp Петpович вопль соседа?
112: Петя составил пpо своих дpузей задачу:
За моими дpузьями гонится двоpник с метлой. Дpузья, удиpая от двоpника, бегают вокpуг дома. Длина дома 170м, шиpина 60 м. Сколько метpов пpобегут мои дpузья, если обегут дом 20 pаз?
113: Дpузья составили задачу пpо Петю:
Hаш дpуг Петя попался нам вечеpком, и каждый из нас дал ему 3 pаза по шее.
Всего наш дpуг Петя получил по шее 108 pаз. Сколько нас было?
117: Допустим, что ты pешил пpыгнуть в воду с высоты 8 метpов и, пpолетев
5 метpов, пеpедумал. Сколько метpов пpидется тебе еще лететь поневоле?
143: Личный попугай капитана Флинта изучил 1567 pугательств на pазных языках.
271 pугательство на английском, 352 на фpанцузском и 127 на испанском языках.
Остальные pугательства попугай подчеpпнул из великого и могучего pусского языка.
Сколько pугательств подчеpпнул личный попугай капитана Флинта из pусского языка?
158: Кощей Бессмеpтный, Баба Яга и Змей Гоpыныч выпили соpокаведеpную бочку пепсиколы. Кощей выпил 6 ведеp, Баба Яга - 4, а остальное честно pазделил между собой тpехголовый Змей Гоpыныч. По сколько ведеp пепсиколы досталось каждой голове?
163: Муха, ползущая от кончика носа дяди Гоши к пеpеносице, пpоходит это pасстояние за 2 минуты. Скоpость мухи 9 см в минуту. Узнай дядю Гошу.
166: 40 бабушек вошли в автобус. пятая часть бабушек купила билеты, а остальные закpичали, что у них пpоездной. Hа самом деле пpоездной был только у семи бабушек. Сколько бабушек поехали зайцем?
170: Федя с одноклассникамми и учительницей пошел на эксуpсию в ботанический сад и там пpисел отдохнуть на кактус. 27 колючек он сумел вытащить из себя сам. 26 колючек достала из него учителница. Каждый из 24 его одноклассников вынул из Феди по 12 колючек. Оставшиеся 187 штук помогли добыть дpугие посетители ботанического сада. Узнай, сколько колючек тоpчало из кактуса до того, как Федя пpисел на него отдохнуть, если во вpемя этого события кактус pасстался с тpетьей частью колючек?
180: Один дедушка охотлся в кухне на таpаканов и убил пятеpых, а pанил в тpи pаза больше. Тpех таpаканов дедушка pанил смеpтельно, и они погибли от pан, а остальные pаненые таpаканы выздоpовели, но обиделись на дедушку и навсегда ушли к соседям. Сколько таpаканов ушли к соседям навсегда?
181: Однажды темной ночью таpаканы собpались на кухне и постpоились в колонну.
Получилось 8 pядов по 7 таpаканов в каждом pяду. Сколько таpаканов собpадось на кухне в эту темную ночь?
190: За столом сидели 16 наpядных гостей и хозяйка дома с двухлетней Машей на pуках. 3 гостя успели выскочить из за стола до того, как Маша вооpужилась винигpетом. Остальные гости попали под обстpел. Сколько гостей постpадало от обстpела винигpетом?
209: Отплякиваясь от суpых пляк, каждый хамсик шмыpяет на глын по 5 гнусиков.
Сколько гнусиков шмыpнут на глын 12 хамсиков, отплякивающихся от суpых пляк?
229: Вовочка 10 pаз деpнул за косичку Машу, 5 pаз Дашу, 7 pаз Клаву и 1 pаз, по ошибке, завуча Маpгаpиту Багpатионовну. Спpашивается: сколько pаз деpгал Вовочка за косички и что тепеpь будет?
268: Баба Яга утвеpждает, что Змей Гоpыныч не пpолетит 1000 км без дозапpавки.
Кощей Бессмеpтный поспоpил с ней на бочку кваса, что пpолетит. Змей Гоpыныч пpолетел 4 часа со скоpостью 247 км/ч и, совеpшив вынужденную посадку, съел Ивана Цаpевича. Пpоспоpила Баба Яга бочку кваса или не пpоспоpила?
286: Два киpпча летели с одинаковой скоpостью, хотя и был бpошены pазными мальчиками дpуг в дpуга. К счастью, оба киpпича пpомахнулись. Пеpвый киpпич был в воздухе 8 секунд, а втоpой на 2 секунды меньше. Втоpой киpпич пpолетел больше пеpвого на 6 м. Какое pасстояние пpолетел каждый киpпич?
301: Петp Петpович пpишел посовтоваться к Машиному папе, снял в коpидоpе ботинки и надел тапочки. Как только тpехлетняя Маша обнаpужила в коpидоpе пустые ботинки Петpа Петpовича, она сpазу же наложила в каждый по 6 ложек манной каши. Сколько ложек манной каши обнаpужил в своих ботинках Петp Петpович после того, как получил дельный совет?
324: Маленькая девочка заблудилась в лесу, зашла в избушку, где жили тpи медведя, и пеpеломала там всю мебель. Сколько пpедметов сломала маленькая девочка, если известно, что у бедных медведей всго-то и было: тpи кpовати, тpи стула и один стол?
Задания Олимпиады Сократ
Задача 1. Шахматный Клуб Зверей
Однажды, в субботу вечером Винни Пух и Тигра решили отдохнуть и поиграть в шахматы в Шахматном Клубе Зверей.
Они оба сыграли по несколько партий.
К своему великому изумлению, Винни Пух ни разу не проиграл, а даже выиграл две партии, а три партии свел в ничью.
Тигра выиграл три партии и три партии проиграл.
Чему равно самое маленькое число игр, которое могли сыграть Винни Пух и Тигра всего в этот вечер?
Задача 2. Посчитаем черепашек на Олимпийских Играх Зверей!
В команде рептилий были только черепашки. Черепашек было больше 50-ти, но меньше 100.
На церемонии открытия Олимпийских Игр Зверей эту команду никак не удавалось построить рядами по 2, 3, или 4 животных, так как одного животного всегда не хватало в последнем ряду.
Поэтому пришлось построить команду черепашек рядами по 5 животных в каждом ряду.
Сколько всего черепашек было в команде рептилий?
Задача 3. Соревнование и конфеты
Анна, Лада и Диана устроили соревнование по бегу на роликовых коньках.
Вначале у всех было одинаковое количество конфет, но после каждого забега девочка, прибежавшая последней, отдавала девочке, занявшей первое место - 2 конфетки, а девочке, занявшей 2-ое место - 1 конфетку.
Не было ни одного забега, в котором первое или второе место заняли бы две девочки.
После 5-ти забегов у Анны стало 18 конфеток, у Лады - 8 конфеток, у Дианы - 4 конфетки.
Сколько раз каждая девочка занимала 1-ое, 2 -ое или 3-е место?
Задача 4. Кто угнал машину?
В некотором городе живут три типа людей: такие, которые всегда говорят правду (правдолюбцы), всегда говорят неправду (лжецы), и шутники, в зависимости от настроения, говорят либо правду, либо неправду.
В этом городе кто-то угнал машину у градоначальника. Полиция задержала троих человек: Джона, Джека и Джо.
Полиции было известно, что один из них - лжец, один - всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь.
Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду.
Три человека сказали следующее:
Джон: Я не виновен.
Джек: Он говорит истинную правду.
Джо: Я угнал машину.
Кто угнал машину и кто лжец?
Задача 5. Ищем зеркальную пару чисел
Два числа называются зеркальной парой чисел, если порядок цифр в одном из них слева направо такой же самый, как порядок цифр другого числа справа налево.
Произведение какой зеркальной пары чисел равно 92565?
Задача 6. Математический ребус!
Однажды, в субботу вечером Винни Пух и Тигра решили отдохнуть и поиграть в шахматы в Шахматном Клубе Зверей.
Они оба сыграли по несколько партий.
К своему великому изумлению, Винни Пух ни разу не проиграл, а даже выиграл две партии, а три партии свел в ничью.
Тигра выиграл три партии и три партии проиграл.
Чему равно самое маленькое число игр, которое могли сыграть Винни Пух и Тигра всего в этот вечер?
Задача 2. Посчитаем черепашек на Олимпийских Играх Зверей!
В команде рептилий были только черепашки. Черепашек было больше 50-ти, но меньше 100.
На церемонии открытия Олимпийских Игр Зверей эту команду никак не удавалось построить рядами по 2, 3, или 4 животных, так как одного животного всегда не хватало в последнем ряду.
Поэтому пришлось построить команду черепашек рядами по 5 животных в каждом ряду.
Сколько всего черепашек было в команде рептилий?
Задача 3. Соревнование и конфеты
Анна, Лада и Диана устроили соревнование по бегу на роликовых коньках.
Вначале у всех было одинаковое количество конфет, но после каждого забега девочка, прибежавшая последней, отдавала девочке, занявшей первое место - 2 конфетки, а девочке, занявшей 2-ое место - 1 конфетку.
Не было ни одного забега, в котором первое или второе место заняли бы две девочки.
После 5-ти забегов у Анны стало 18 конфеток, у Лады - 8 конфеток, у Дианы - 4 конфетки.
Сколько раз каждая девочка занимала 1-ое, 2 -ое или 3-е место?
Задача 4. Кто угнал машину?
В некотором городе живут три типа людей: такие, которые всегда говорят правду (правдолюбцы), всегда говорят неправду (лжецы), и шутники, в зависимости от настроения, говорят либо правду, либо неправду.
В этом городе кто-то угнал машину у градоначальника. Полиция задержала троих человек: Джона, Джека и Джо.
Полиции было известно, что один из них - лжец, один - всегда говорит правду, а про третьего точно неизвестно, говорит ли он правду или ложь.
Полиция также знала, что один из них угнал машину, и что этот человек всегда говорит правду.
Три человека сказали следующее:
Джон: Я не виновен.
Джек: Он говорит истинную правду.
Джо: Я угнал машину.
Кто угнал машину и кто лжец?
Задача 5. Ищем зеркальную пару чисел
Два числа называются зеркальной парой чисел, если порядок цифр в одном из них слева направо такой же самый, как порядок цифр другого числа справа налево.
Произведение какой зеркальной пары чисел равно 92565?
Задача 6. Математический ребус!
Домино из шахматной доски
Если из шахматной доски вырезать 2 угловых поля, лежащих на одной диагонали, то её станет невозможно полностью разрезать на "доминошки" 1x2.
Казалось бы, почему невозможно? Ведь остаётся 62 клетки, число чётное, и вполне может быть покрытое 31-й плиткой домино. Однако стоит вспомнить о раскраске. Среди оставшихся полей 30 белых и 32 чёрных. Доминошка же, как её ни располагай, будет всегда вмещать одно чёрное и одно белое поле. Таким образом, после того как вырежем из доски 30 плиток, останутся 2 несвязанные чёрные клетки.
Казалось бы, почему невозможно? Ведь остаётся 62 клетки, число чётное, и вполне может быть покрытое 31-й плиткой домино. Однако стоит вспомнить о раскраске. Среди оставшихся полей 30 белых и 32 чёрных. Доминошка же, как её ни располагай, будет всегда вмещать одно чёрное и одно белое поле. Таким образом, после того как вырежем из доски 30 плиток, останутся 2 несвязанные чёрные клетки.
Математика в художественном слове
МАТЕМАТИЧЕСКИЕ ПОСЛОВИЦЫ И ПОГОВОРКИ
ОДИН в поле не воин.
ОДИН, как красное солнышко.
ОДИН, как ясный месяц.
ОДИН, как медведь в берлоге.
ОДИН с сошкой, СЕМЕРО с ложкой.
Лучше ОДИН раз увидеть, чем СТО раз услышать.
ОДНА ласточка весны не делает.
ОДНА пчела МНОГО меду не натаскает.
ОДНА голова - хорошо, а ДВЕ - лучше.
ОДНОМУ ехать и дорога долга.
ОДНОМУ страшно, а ораве все нипочем.
Клади по ОДНОЙ ягодке - наберешь кузовок.
Все за ОДНОГО, ОДИН за всех, тогда в деле будет успех
Ум - хорошо, ДВА - лучше.
ДВА сапога ПАРА.
ДВА глаза дороже алмаза.
ДВА друга - метель и вьюга.
Над лесом дождь ДВАЖДЫ идет,
Больше ДВУХ - говорят вслух.
Старый друг лучше новых ДВУХ.
За ДВУМЯ зайцами погонишься, НИ ОДНОГО не поймаешь.
Чтобы научиться трудолюбию, нужно ТРИ ГОДА,
Чтобы научиться лени - только ТРИ ДНЯ.
ЯКИМ-простота, ДВЕ рукавицы за поясом, а ТРЕТЬЮ ищет.
Без ЧЕТЫРЕХ углов изба не рубится.
Конь о ЧЕТЫРЕХ ногах - и тот спотыкается.
Лук СЕМЬ недугов лечит, а чеснок СЕМЬ недугов изводит.
СЕМЬ ПЯТНИЦ на НЕДЕЛЕ.
СЕМЬ раз отмерь, ОДИН раз отрежь.
СЕМЬ бед, ОДИН ответ.
ОДИН с сошкой, СЕМЕРО с ложкой.
СЕМЕРО ОДНОГО не ждут.
У СЕМИ нянек дитя без глаза.
ОСЕНЬ - перемен ВОСЕМЬ.
ВЕСНА да ОСЕНЬ - на дню погод ВОСЕМЬ.
ОДИН работает, ДЕСЯТЬ - погоняют.
Не имей СТО рублей, а имей СТО друзей.
ГРОША не стоит, а выглядит РУБЛЕМ.
МНОГО леса - береги, МАЛО леса - не руби, нет леса - посади.
Где МНОГО пташек, там МАЛО букашек.
Знай БОЛЬШЕ, говори МЕНЬШЕ.
Чем БОЛЬШЕ рук, тем легче труд.
ПРАВАЯ рука сильнее ЛЕВОЙ. .
Шутке - МИНУТКА, а делу - ЧАС.
ОДИН в поле не воин.
ОДИН, как красное солнышко.
ОДИН, как ясный месяц.
ОДИН, как медведь в берлоге.
ОДИН с сошкой, СЕМЕРО с ложкой.
Лучше ОДИН раз увидеть, чем СТО раз услышать.
ОДНА ласточка весны не делает.
ОДНА пчела МНОГО меду не натаскает.
ОДНА голова - хорошо, а ДВЕ - лучше.
ОДНОМУ ехать и дорога долга.
ОДНОМУ страшно, а ораве все нипочем.
Клади по ОДНОЙ ягодке - наберешь кузовок.
Все за ОДНОГО, ОДИН за всех, тогда в деле будет успех
Ум - хорошо, ДВА - лучше.
ДВА сапога ПАРА.
ДВА глаза дороже алмаза.
ДВА друга - метель и вьюга.
Над лесом дождь ДВАЖДЫ идет,
Больше ДВУХ - говорят вслух.
Старый друг лучше новых ДВУХ.
За ДВУМЯ зайцами погонишься, НИ ОДНОГО не поймаешь.
Чтобы научиться трудолюбию, нужно ТРИ ГОДА,
Чтобы научиться лени - только ТРИ ДНЯ.
ЯКИМ-простота, ДВЕ рукавицы за поясом, а ТРЕТЬЮ ищет.
Без ЧЕТЫРЕХ углов изба не рубится.
Конь о ЧЕТЫРЕХ ногах - и тот спотыкается.
Лук СЕМЬ недугов лечит, а чеснок СЕМЬ недугов изводит.
СЕМЬ ПЯТНИЦ на НЕДЕЛЕ.
СЕМЬ раз отмерь, ОДИН раз отрежь.
СЕМЬ бед, ОДИН ответ.
ОДИН с сошкой, СЕМЕРО с ложкой.
СЕМЕРО ОДНОГО не ждут.
У СЕМИ нянек дитя без глаза.
ОСЕНЬ - перемен ВОСЕМЬ.
ВЕСНА да ОСЕНЬ - на дню погод ВОСЕМЬ.
ОДИН работает, ДЕСЯТЬ - погоняют.
Не имей СТО рублей, а имей СТО друзей.
ГРОША не стоит, а выглядит РУБЛЕМ.
МНОГО леса - береги, МАЛО леса - не руби, нет леса - посади.
Где МНОГО пташек, там МАЛО букашек.
Знай БОЛЬШЕ, говори МЕНЬШЕ.
Чем БОЛЬШЕ рук, тем легче труд.
ПРАВАЯ рука сильнее ЛЕВОЙ. .
Шутке - МИНУТКА, а делу - ЧАС.
Примерные билеты по геометрии для выпускников 9 классов общеобразовательных учреждений Российской Федерации
Примерные билеты по геометрии
для выпускников 9 классов общеобразовательных
учреждений Российской Федерации
Билет № 1
1. Сформулируйте определение окружности, вписанной в треугольник.
Сформулируйте теорему о центре вписанной окружности. Приведите пример применения теоремы о центре вписанной окружности.
2. Сформулируйте определение трапеции. Сформулируйте определение средней линии трапеции. Сформулируйте и докажите теорему о средней линии трапеции.
3. Задача:
Сторона правильного шестиугольника, описанного около окружности,
равна 2 см. Найдите сторону правильного треугольника, вписанного в эту
окружность.
4. Задача:
В треугольник ABC вписан равнобедренный прямоугольный треугольник DEF так, что его гипотенуза DF параллельна стороне АС, а вершина Е
лежит на стороне АС. Найдите высоту треугольника ABC, если AС = 16 см;
DF = 8 см.
Билет № 2
1. Сформулируйте определение синуса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение равнобедренного треугольника. Сформулируйте и докажите признак равнобедренного треугольника.
3. Задача:
Стороны треугольника равны 3 см, 2 см и 3 см. Определите вид этого
треугольника.
4. Задача:
На стороне АВ параллелограмма АВСD как на диаметре построена
окружность, проходящая через точку пересечения диагоналей и середину
стороны AD. Найдите углы параллелограмма.
Билет № 3
1. Сформулируйте теорему Фалеса. Приведите пример ее применения.
2. Сформулируйте определение равнобедренного треугольника. Сформулируйте и докажите свойство углов при основании равнобедренного
треугольника.
3. Задача:
Угол между высотами BK и BL параллелограмма АВСD, проведенными
из вершины его острого угла B, в четыре раза больше самого угла АВС.
Найдите углы параллелограмма.
4. Задача:
Через вершину В равнобедренного треугольника АВС параллельно
основанию АС проведена прямая ВD. Через точку К – середину высоты ВH
проведен луч АК, пересекающий прямую ВD в точке D, а сторону ВС в точке
N. Определите, в каком отношении точка N делит сторону ВС.
Билет № 4
1. Сформулируйте определение окружности. Приведите формулу длины
окружности. Приведите формулу длины дуги окружности. Приведите примеры применения либо формулы длины окружности, либо формулы длины
дуги окружности.
2. Сформулируйте определение медианы треугольника. Сформулируйте и докажите свойство медианы равнобедренного треугольника.
3. Задача:
Сторона ромба равна 10, а один из его углов равен 30°. Найдите радиус
окружности, вписанной в ромб.
4. Задача:
Одна из диагоналей прямоугольной трапеции делит эту трапецию на
два прямоугольных равнобедренных треугольника. Какова площадь этой
трапеции, если ее меньшая боковая сторона равна 4?
Билет № 5
1. Сформулируйте неравенство треугольника. Приведите пример его
применения.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойство диагоналей параллелограмма.
3. Задача:
Найдите больший угол треугольника, если две его стороны видны из
центра описанной окружности под углами 100° и 120°.
4. Задача:
Известно, что в равнобокую трапецию с боковой стороной, равной 5,
можно вписать окружность. Найдите длину средней линии трапеции.
Билет № 6
1. Приведите формулы площади прямоугольника и площади параллелограмма. Приведите примеры применения площади прямоугольника
либо площади параллелограмма.
2. Сформулируйте определение равных треугольников. Сформулируйте
признаки равенства треугольников и докажите один из них по выбору.
3. Задача:
Определите вид четырехугольника, вершины которого являются серединами сторон произвольного выпуклого четырехугольника.
4. Задача:
В треугольник АВС вписана окружность, которая касается сторон АВ
и ВС в точках E и F соответственно. Касательная MK к этой окружности
пересекает стороны АВ и ВС соответственно в точках M и K. Найдите
периметр треугольника ВMK, если BE = 6 см.
Билет № 7
1. Приведите формулы для радиусов вписанных и описанных окружностей правильных многоугольников. Приведите пример их применения для
N угольников для любого n ≤ 6 (n определяет учащийся).
2. Сформулируйте определение параллельных прямых. Сформулируйте
аксиому параллельных прямых. Сформулируйте признаки параллельности
прямых и докажите один из них по выбору.
3. Задача:
В трапеции ABCD диагональ BD является биссектрисой прямого угла
ADC. Найдите отношение диагонали BD к стороне AB трапеции, если
∠ BAD = 30°.
4. Задача:
Треугольник АBC, стороны которого 13 см,14 см и 15 см, разбит на три
треугольника отрезками, соединяющими точку пересечения медиан М
с вершинами треугольника. Найдите площадь треугольника BMC.
Билет № 8
1. Сформулируйте определения круга и сектора. Приведите формулы
площади круга и площади сектора. Приведите пример применения одной
из формул: либо площади круга, либо площади сектора по выбору учащегося.
2. Сформулируйте определение прямоугольного треугольника. Сформулируйте и докажите теорему Пифагора.
3. Задача:
Площадь треугольника, описанного около окружности, равна 84 см2.
Найдите периметр треугольника, если радиус окружности равен 7 см.
4. Задача:
В равнобокой трапеции одно из оснований в два раза больше другого.
Диагональ трапеции является биссектрисой острого угла. Найдите меньшее основание трапеции, если ее площадь равна 27 __3_ см2.
Билет № 9
1. Сформулируйте определение окружности, описанной около треугольника. Сформулируйте теорему о центре описанной окружности. Приведите
пример применения теоремы о центре описанной окружности.
2. Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.
3. Задача:
Из вершины B в треугольнике ABC проведены высота BH и биссектриса BD. Найдите угол между высотой BH и биссектрисой BD, если углы BAC
и BCA равны 20° и 60° соответственно.
4. Задача:
Две окружности, радиусы которых равны 9 см и 3 см, касаются внешним
образом в точке А. Через точку А проходит их общая секущая ВС, причем
точка В принадлежит большей окружности. Найдите длину отрезка AB, если
отрезок AC равен 5 см.
Билет № 10
1. Сформулируйте теорему о сумме углов треугольника. Приведите
пример ее применения.
2. Сформулируйте определение ромба. Сформулируйте и докажите
свойство диагоналей ромба.
3. Задача:
Внутри равностороннего треугольника ABC отмечена точка D, такая, что
∠ BAD = ∠ BCD = 15°. Найдите угол ADC.
4. Задача:
Окружность радиуса R касается гипотенузы равнобедренного прямоугольного треугольника в вершине его острого угла и проходит через вершину прямого угла. Найдите длину дуги, заключенной внутри треугольника, если R =8—π.
Билет № 11
1. Сформулируйте определение выпуклого многоугольника. Сформулируйте теорему о сумме углов выпуклого многоугольника. Приведите пример
ее применения.
2. Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.
3. Задача:
Через вершины А, В и С ромба АВСО проведена окружность, центром
которой является вершина О. Найдите длину дуги АС, содержащей вершину
В, если длина всей окружности равна 30 см.
4. Задача:
При пересечении двух прямых n и m секущей k образовалось восемь
углов. Четыре из них равны 60°, а четыре другие – 120°. Определите взаимное расположение прямых n и m.
Билет № 12
1. Приведите формулы площади треугольника. Приведите примеры их
применения.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите признак параллелограмма по выбору учащегося.
3. Задача:
Точки A, B и C делят окружность на три части так, что ∪AB : ∪BC : ∪AC =
= 4 : 7 : 9. Определите наибольший угол треугольника ABC.
4. Задача:
Углы при основании AD трапеции ABCD равны 60° и 30°, AD = 17 см,
ВС = 7 см. Найдите боковые стороны.
Билет № 13
1. Сформулируйте определение тангенса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойства углов и сторон параллелограмма.
3. Задача:
Длины двух сторон равнобедренного треугольника равны соответственно 6 см и 2 см. Определите длину третьей стороны этого треугольника.
4. Задача:
Два круга, радиусы которых равны 5 см, имеют общую хорду длины
5 см. Найдите площадь общей части этих кругов.
Билет № 14
1. Сформулируйте определение внешнего угла треугольника. Сформулируйте теорему о свойстве внешнего угла треугольника. Приведите пример ее применения.
2. Сформулируйте и докажите теорему косинусов. Приведите пример
ее применения для решения треугольников.
3. Задача:
Стороны треугольника равны 4 см, 5 см и 8 см. Найдите длину медианы, проведенной из вершины большего угла.
4. Задача:
В параллелограмме АВСD диагональ BD перпендикулярна стороне AD.
Найдите АС, если AD = 6 см, BD = 5 см.
Билет № 15
1. Приведите формулу площади трапеции. Приведите пример ее применения.
2. Сформулируйте определение равных треугольников. Сформулируйте
признаки равенства прямоугольных треугольников и докажите один из них
по выбору.
3. Задача:
Большая диагональ ромба равна 12 см, а один из его углов равен 60°.
Найдите длину вписанной в него окружности.
4. Задача:
В равнобедренном треугольнике центр вписанной окружности делит
высоту в отношении 17 : 15, а боковая сторона равна 34 см. Найдите основание треугольника.
Билет № 16
1. Сформулируйте теорему о зависимости между сторонами и углами
треугольника. Приведите пример ее применения.
2. Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников и докажите один из них по выбору.
3. Задача:
Найдите меньший угол параллелограмма, если его стороны равны
1 и 3, а одна из диагоналей равна 7.
4. Задача:
В треугольник АВС вписан квадрат так, что две его вершины лежат на
стороне АB и по одной вершине – на сторонах АC и ВС. Найдите площадь
квадрата, если АB = 40 см, а высота, проведенная из вершины С, имеет
длину 24 см.
Билет № 17
1. Сформулируйте определение вектора. Сформулируйте определение
суммы векторов. Сформулируйте свойства сложения векторов. Приведите
примеры сложения векторов.
2. Сформулируйте и докажите теорему синусов. Приведите пример ее
применения для решения треугольников.
3. Задача:
Вписанный угол, образованный хордой и диаметром окружности, равен
72°. Определите, что больше: хорда или радиус окружности.
4. Задача:
В трапеции АВСD стороны АВ и СD равны, биссектриса тупого угла В
перпендикулярна диагонали АС и отсекает от данной трапеции параллелограмм. Найдите величину угла ВСD.
Билет № 18
1. Сформулируйте определение вектора. Сформулируйте определение
произведения вектора на число. Сформулируйте свойства произведения
вектора на число. Приведите примеры произведения вектора на число.
2. Сформулируйте определения центрального угла окружности и угла,
вписанного в окружность. Сформулируйте и докажите теорему об измерении вписанного угла.
3. Задача:
Медиана ВМ треугольника АВС перпендикулярна его биссектрисе АD.
Найдите АВ, если АС = 12 см.
4. Задача:
В прямоугольной трапеции ABCD с основаниями 17 см и 25 см диагональ AC является биссектрисой острого угла A. Найдите меньшую боковую
сторону трапеции.
Билет № 19
1. Сформулируйте определение скалярного произведения векторов и
определение угла между векторами. Приведите пример применения скалярного произведения векторов для определения угла между векторами.
2. Сформулируйте определение серединного перпендикуляра к отрезку.
Сформулируйте и докажите свойство серединного перпендикуляра к отрезку.
3. Задача:
4. Задача:
Треугольник АВС – равносторонний со стороной, равной а. На расстоянии а от вершины А взята точка D, отличная от точек В и С. Найдите угол
BDC.
Билет № 20
1. Сформулируйте свойство углов, образованных при пересечении параллельных прямых секущей. Приведите пример вычисления углов при
пересечении параллельных прямых секущей.
2. Сформулируйте теоремы о пропорциональных отрезках в прямоугольном треугольнике и докажите один из них по выбору.
3. Задача:
Из точки, лежащей на гипотенузе равнобедренного прямоугольного треугольника, на катеты треугольника опущены перпендикуляры. Найдите катет
треугольника, если периметр полученного четырехугольника равен 12 см.
4. Задача:
Около правильного шестиугольника со стороной 8,5 описана окружность. Около этой окружности описан правильный четырехугольник. Найдите сторону четырехугольника.
Билет № 21
1. Сформулируйте определение косинуса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение биссектрисы угла. Сформулируйте
и докажите свойство биссектрисы треугольника.
3. Задача:
Площадь ромба ABCD равна 242 см2. Вычислите сторону ромба, если
один из его углов равен 135°.
4. Задача:
К окружности, радиус которой равен 3, из точки, удаленной от центра
окружности на расстояние 5, проведены две касательные. Вычислите расстояние между точками касания.
для выпускников 9 классов общеобразовательных
учреждений Российской Федерации
Билет № 1
1. Сформулируйте определение окружности, вписанной в треугольник.
Сформулируйте теорему о центре вписанной окружности. Приведите пример применения теоремы о центре вписанной окружности.
2. Сформулируйте определение трапеции. Сформулируйте определение средней линии трапеции. Сформулируйте и докажите теорему о средней линии трапеции.
3. Задача:
Сторона правильного шестиугольника, описанного около окружности,
равна 2 см. Найдите сторону правильного треугольника, вписанного в эту
окружность.
4. Задача:
В треугольник ABC вписан равнобедренный прямоугольный треугольник DEF так, что его гипотенуза DF параллельна стороне АС, а вершина Е
лежит на стороне АС. Найдите высоту треугольника ABC, если AС = 16 см;
DF = 8 см.
Билет № 2
1. Сформулируйте определение синуса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение равнобедренного треугольника. Сформулируйте и докажите признак равнобедренного треугольника.
3. Задача:
Стороны треугольника равны 3 см, 2 см и 3 см. Определите вид этого
треугольника.
4. Задача:
На стороне АВ параллелограмма АВСD как на диаметре построена
окружность, проходящая через точку пересечения диагоналей и середину
стороны AD. Найдите углы параллелограмма.
Билет № 3
1. Сформулируйте теорему Фалеса. Приведите пример ее применения.
2. Сформулируйте определение равнобедренного треугольника. Сформулируйте и докажите свойство углов при основании равнобедренного
треугольника.
3. Задача:
Угол между высотами BK и BL параллелограмма АВСD, проведенными
из вершины его острого угла B, в четыре раза больше самого угла АВС.
Найдите углы параллелограмма.
4. Задача:
Через вершину В равнобедренного треугольника АВС параллельно
основанию АС проведена прямая ВD. Через точку К – середину высоты ВH
проведен луч АК, пересекающий прямую ВD в точке D, а сторону ВС в точке
N. Определите, в каком отношении точка N делит сторону ВС.
Билет № 4
1. Сформулируйте определение окружности. Приведите формулу длины
окружности. Приведите формулу длины дуги окружности. Приведите примеры применения либо формулы длины окружности, либо формулы длины
дуги окружности.
2. Сформулируйте определение медианы треугольника. Сформулируйте и докажите свойство медианы равнобедренного треугольника.
3. Задача:
Сторона ромба равна 10, а один из его углов равен 30°. Найдите радиус
окружности, вписанной в ромб.
4. Задача:
Одна из диагоналей прямоугольной трапеции делит эту трапецию на
два прямоугольных равнобедренных треугольника. Какова площадь этой
трапеции, если ее меньшая боковая сторона равна 4?
Билет № 5
1. Сформулируйте неравенство треугольника. Приведите пример его
применения.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойство диагоналей параллелограмма.
3. Задача:
Найдите больший угол треугольника, если две его стороны видны из
центра описанной окружности под углами 100° и 120°.
4. Задача:
Известно, что в равнобокую трапецию с боковой стороной, равной 5,
можно вписать окружность. Найдите длину средней линии трапеции.
Билет № 6
1. Приведите формулы площади прямоугольника и площади параллелограмма. Приведите примеры применения площади прямоугольника
либо площади параллелограмма.
2. Сформулируйте определение равных треугольников. Сформулируйте
признаки равенства треугольников и докажите один из них по выбору.
3. Задача:
Определите вид четырехугольника, вершины которого являются серединами сторон произвольного выпуклого четырехугольника.
4. Задача:
В треугольник АВС вписана окружность, которая касается сторон АВ
и ВС в точках E и F соответственно. Касательная MK к этой окружности
пересекает стороны АВ и ВС соответственно в точках M и K. Найдите
периметр треугольника ВMK, если BE = 6 см.
Билет № 7
1. Приведите формулы для радиусов вписанных и описанных окружностей правильных многоугольников. Приведите пример их применения для
N угольников для любого n ≤ 6 (n определяет учащийся).
2. Сформулируйте определение параллельных прямых. Сформулируйте
аксиому параллельных прямых. Сформулируйте признаки параллельности
прямых и докажите один из них по выбору.
3. Задача:
В трапеции ABCD диагональ BD является биссектрисой прямого угла
ADC. Найдите отношение диагонали BD к стороне AB трапеции, если
∠ BAD = 30°.
4. Задача:
Треугольник АBC, стороны которого 13 см,14 см и 15 см, разбит на три
треугольника отрезками, соединяющими точку пересечения медиан М
с вершинами треугольника. Найдите площадь треугольника BMC.
Билет № 8
1. Сформулируйте определения круга и сектора. Приведите формулы
площади круга и площади сектора. Приведите пример применения одной
из формул: либо площади круга, либо площади сектора по выбору учащегося.
2. Сформулируйте определение прямоугольного треугольника. Сформулируйте и докажите теорему Пифагора.
3. Задача:
Площадь треугольника, описанного около окружности, равна 84 см2.
Найдите периметр треугольника, если радиус окружности равен 7 см.
4. Задача:
В равнобокой трапеции одно из оснований в два раза больше другого.
Диагональ трапеции является биссектрисой острого угла. Найдите меньшее основание трапеции, если ее площадь равна 27 __3_ см2.
Билет № 9
1. Сформулируйте определение окружности, описанной около треугольника. Сформулируйте теорему о центре описанной окружности. Приведите
пример применения теоремы о центре описанной окружности.
2. Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.
3. Задача:
Из вершины B в треугольнике ABC проведены высота BH и биссектриса BD. Найдите угол между высотой BH и биссектрисой BD, если углы BAC
и BCA равны 20° и 60° соответственно.
4. Задача:
Две окружности, радиусы которых равны 9 см и 3 см, касаются внешним
образом в точке А. Через точку А проходит их общая секущая ВС, причем
точка В принадлежит большей окружности. Найдите длину отрезка AB, если
отрезок AC равен 5 см.
Билет № 10
1. Сформулируйте теорему о сумме углов треугольника. Приведите
пример ее применения.
2. Сформулируйте определение ромба. Сформулируйте и докажите
свойство диагоналей ромба.
3. Задача:
Внутри равностороннего треугольника ABC отмечена точка D, такая, что
∠ BAD = ∠ BCD = 15°. Найдите угол ADC.
4. Задача:
Окружность радиуса R касается гипотенузы равнобедренного прямоугольного треугольника в вершине его острого угла и проходит через вершину прямого угла. Найдите длину дуги, заключенной внутри треугольника, если R =8—π.
Билет № 11
1. Сформулируйте определение выпуклого многоугольника. Сформулируйте теорему о сумме углов выпуклого многоугольника. Приведите пример
ее применения.
2. Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.
3. Задача:
Через вершины А, В и С ромба АВСО проведена окружность, центром
которой является вершина О. Найдите длину дуги АС, содержащей вершину
В, если длина всей окружности равна 30 см.
4. Задача:
При пересечении двух прямых n и m секущей k образовалось восемь
углов. Четыре из них равны 60°, а четыре другие – 120°. Определите взаимное расположение прямых n и m.
Билет № 12
1. Приведите формулы площади треугольника. Приведите примеры их
применения.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите признак параллелограмма по выбору учащегося.
3. Задача:
Точки A, B и C делят окружность на три части так, что ∪AB : ∪BC : ∪AC =
= 4 : 7 : 9. Определите наибольший угол треугольника ABC.
4. Задача:
Углы при основании AD трапеции ABCD равны 60° и 30°, AD = 17 см,
ВС = 7 см. Найдите боковые стороны.
Билет № 13
1. Сформулируйте определение тангенса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение параллелограмма. Сформулируйте
и докажите свойства углов и сторон параллелограмма.
3. Задача:
Длины двух сторон равнобедренного треугольника равны соответственно 6 см и 2 см. Определите длину третьей стороны этого треугольника.
4. Задача:
Два круга, радиусы которых равны 5 см, имеют общую хорду длины
5 см. Найдите площадь общей части этих кругов.
Билет № 14
1. Сформулируйте определение внешнего угла треугольника. Сформулируйте теорему о свойстве внешнего угла треугольника. Приведите пример ее применения.
2. Сформулируйте и докажите теорему косинусов. Приведите пример
ее применения для решения треугольников.
3. Задача:
Стороны треугольника равны 4 см, 5 см и 8 см. Найдите длину медианы, проведенной из вершины большего угла.
4. Задача:
В параллелограмме АВСD диагональ BD перпендикулярна стороне AD.
Найдите АС, если AD = 6 см, BD = 5 см.
Билет № 15
1. Приведите формулу площади трапеции. Приведите пример ее применения.
2. Сформулируйте определение равных треугольников. Сформулируйте
признаки равенства прямоугольных треугольников и докажите один из них
по выбору.
3. Задача:
Большая диагональ ромба равна 12 см, а один из его углов равен 60°.
Найдите длину вписанной в него окружности.
4. Задача:
В равнобедренном треугольнике центр вписанной окружности делит
высоту в отношении 17 : 15, а боковая сторона равна 34 см. Найдите основание треугольника.
Билет № 16
1. Сформулируйте теорему о зависимости между сторонами и углами
треугольника. Приведите пример ее применения.
2. Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников и докажите один из них по выбору.
3. Задача:
Найдите меньший угол параллелограмма, если его стороны равны
1 и 3, а одна из диагоналей равна 7.
4. Задача:
В треугольник АВС вписан квадрат так, что две его вершины лежат на
стороне АB и по одной вершине – на сторонах АC и ВС. Найдите площадь
квадрата, если АB = 40 см, а высота, проведенная из вершины С, имеет
длину 24 см.
Билет № 17
1. Сформулируйте определение вектора. Сформулируйте определение
суммы векторов. Сформулируйте свойства сложения векторов. Приведите
примеры сложения векторов.
2. Сформулируйте и докажите теорему синусов. Приведите пример ее
применения для решения треугольников.
3. Задача:
Вписанный угол, образованный хордой и диаметром окружности, равен
72°. Определите, что больше: хорда или радиус окружности.
4. Задача:
В трапеции АВСD стороны АВ и СD равны, биссектриса тупого угла В
перпендикулярна диагонали АС и отсекает от данной трапеции параллелограмм. Найдите величину угла ВСD.
Билет № 18
1. Сформулируйте определение вектора. Сформулируйте определение
произведения вектора на число. Сформулируйте свойства произведения
вектора на число. Приведите примеры произведения вектора на число.
2. Сформулируйте определения центрального угла окружности и угла,
вписанного в окружность. Сформулируйте и докажите теорему об измерении вписанного угла.
3. Задача:
Медиана ВМ треугольника АВС перпендикулярна его биссектрисе АD.
Найдите АВ, если АС = 12 см.
4. Задача:
В прямоугольной трапеции ABCD с основаниями 17 см и 25 см диагональ AC является биссектрисой острого угла A. Найдите меньшую боковую
сторону трапеции.
Билет № 19
1. Сформулируйте определение скалярного произведения векторов и
определение угла между векторами. Приведите пример применения скалярного произведения векторов для определения угла между векторами.
2. Сформулируйте определение серединного перпендикуляра к отрезку.
Сформулируйте и докажите свойство серединного перпендикуляра к отрезку.
3. Задача:
4. Задача:
Треугольник АВС – равносторонний со стороной, равной а. На расстоянии а от вершины А взята точка D, отличная от точек В и С. Найдите угол
BDC.
Билет № 20
1. Сформулируйте свойство углов, образованных при пересечении параллельных прямых секущей. Приведите пример вычисления углов при
пересечении параллельных прямых секущей.
2. Сформулируйте теоремы о пропорциональных отрезках в прямоугольном треугольнике и докажите один из них по выбору.
3. Задача:
Из точки, лежащей на гипотенузе равнобедренного прямоугольного треугольника, на катеты треугольника опущены перпендикуляры. Найдите катет
треугольника, если периметр полученного четырехугольника равен 12 см.
4. Задача:
Около правильного шестиугольника со стороной 8,5 описана окружность. Около этой окружности описан правильный четырехугольник. Найдите сторону четырехугольника.
Билет № 21
1. Сформулируйте определение косинуса острого угла прямоугольного
треугольника. Приведите пример его применения при решении прямоугольных треугольников.
2. Сформулируйте определение биссектрисы угла. Сформулируйте
и докажите свойство биссектрисы треугольника.
3. Задача:
Площадь ромба ABCD равна 242 см2. Вычислите сторону ромба, если
один из его углов равен 135°.
4. Задача:
К окружности, радиус которой равен 3, из точки, удаленной от центра
окружности на расстояние 5, проведены две касательные. Вычислите расстояние между точками касания.
понедельник, 16 мая 2011 г.
Логическая задача
Из трех пятерок и одной единицы, пользуясь сложением, вычитанием, умножением и делением, получить 24
четверг, 12 мая 2011 г.
Знакомимся с параболой
Задание №1.Что такое парабола?
Как определить направление ветвей?
Как найти нули функции?
Что называется наибольшее и наименьшее значение функции?
Когда фунция возрастает и убывает?
Ответы разместить в моем блоге. Для этого вы должны создать свой аккаунт.
среда, 11 мая 2011 г.
четверг, 5 мая 2011 г.
Учим таблицу квадратов
Выбери тип игры
More educational activitites at StudyStack.comВыучить таблицу квадратов
More educational activitites at StudyStack.com
More educational activitites at StudyStack.comВыучить таблицу квадратов
More educational activitites at StudyStack.com
среда, 4 мая 2011 г.
четверг, 28 апреля 2011 г.
Спортивный класс
В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.
Для решения используйте диаграмму, где большой круг изображает всех учащихся класса,
а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов.
Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта.
Сколько ребят увлекаются одновременно тремя видами спорта?Сколько ребят увлекается лишь одним из этих видов спорта? Ответ отправить на мой блог
среда, 27 апреля 2011 г.
четверг, 21 апреля 2011 г.
четверг, 14 апреля 2011 г.
Подписаться на:
Сообщения (Atom)